Одна из главнейших проблем эволюции — это происхождение информации. Как могло случится, что биологичекие системы, имеющие конкретную цель (в телеологическом смысле), возникли в результате одних только естественных процессов? Не думая о последствиях своих собственных аргументов, эволюционисты долгое время утверждали, что цель это иллюзия. Их логическая последовательность была проста:

1. Порядок ошибочно принимается за цель.
2. Порядок — это результат естественных процессов.
3. Следовательно то, что кажется целью, на самом деле является результатом естественных процессов.

Последний аргумент в пользу этой точки зрения берется из теории сложности, на основе которой Мелани Митчел (Melanie Mitchell) утверждает что:

«Большинство биологов-последователей дарвиновской традиции считают, что порядок онтогенеза обусловлен размалывающим действием молекулярной машины Руба Голдберга, слепленный по кусочкам эволюцией. Я выдвигаю противоположный аргумент: большая часть прекрасного порядка, наблюдаемого в онтогенезе спонтанна и является естественным выражением потрясающей самоорганизации, которой изобилуют очень сложные регуляторные сети. Мы были совершенно неправы. Порядок, огромный и все-порождающий, возникает естественно».¹

Однако опять такой аргумент выдвигается без учета вытекающих из него фактических следствий. Каков же реальный исход аргумента теории сложности? Во-первых, приравнивание сложности к цели разрушает само себя, поскольку подрывает логику, которая нужна для перехода от идеи целенаправленности к идее просто упорядоченной мысли не содержащей смысла. 

Во-вторых, приравнивание сложности к цели убивает всякую надежду объяснить и понять упорядоченную и спланированную сложность. Данная статья посвящена рассмотрению именно этого, второго результата.

Упорядоченная сложность

Наука о сложности, как любят говорить теоретики сложности (в ироническом смысле фразы) — это новая, эмерджентная область исследований («эмерджентность» —  наличие особых свойств системы, не присущих ее элементам — В.М.) . Находя применение в областях от корпоративного финансирования до фондового рынка и социальных сетей, наука о сложности находится на переднем крае современных исследований по вполне понятным причинам. 

В каждой из этих областей исследователи и инженеры открывают и переоткрывают множество одинаковых принципов и идей, сталкиваясь со статьями друг друга, в которых обнаруживаются параллельные места между такими далекими сферами, как компьютерные сети и биология.

Однако, во всех этих областях на пути встает одно и то же препятствие: упорядоченная сложность. В 1948 году Вивер (Weaver) объяснял эту проблему следующим образом:

«Этот новый метод изучения неорганизованной сложности, явившийся мощным прорывом по сравнению с ранее используемыми методами, основанными на двух переменных, оставляет нетронутым большое поле. Появляется соблазн черезмерного упрощения и утверждения, что научная методология перешла из одной крайности в другую — от двух переменных к их астрономическому числу, оставив нетронутым большое промежуточное пространство. Более того, важность промежуточного пространства не зависит от того факта, что число переменных сравнительно невелико — значительно больше двух, но мало по сравнению с числом атомов в щепотке соли. Проблемы в промежуточном районе, на самом деле, часто будут связаны со значительным числом переменных. По настоящему важной характеристикой проблем промежуточного района, который наука еще серьезно не изучила и не покорила, в том, что эти проблемы, в противоположность ситуациям характеризующимися дезорганизацией, поддающейся статистической обработке, демонстрируют фундаментальное свойство организованности. По сути, эту группу проблем можно охарактеризовать как организованную сложность».²

В качестве примера неорганизованной сложности, Вивер приводит бильярдный стол, у которого нет боковых карманов (т. е. шары не могут покинуть этот стол), поверхность не имеет трения, а стенки идеально упругие (рис. 1). Поместим на этот стол десять шаров, которые сталкиваются без потери энергии — другими словами законы термодинамики временно не действуют в отношении стола и шаров. Теперь допустим, что эти десять шаров начинают двигаться случайным образом в разных направлениях.

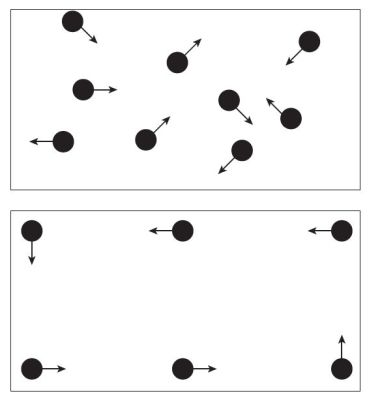Рисунок 1. Два бильярдных стола, как пример неупорядоченной (вверху) и упорядоченной (внизу) сложности.

С помощью довольно простой математики можно подробно предсказать перемещения каждого шара, включая удары о стенки и столкновения с другими шарами. 

Если знать точку старта, энергию и направление движения каждого шара в определенный момент, то можно рассчитать положение и направление движения любого шара в любой момент времени. Удалите все сведения о начальном местоположении, направлении движения и количестве энергии, и попросту наблюдайте за шарами, как они двигаются по столу. 

Тогда потребуется более сложная математика, которая была разработана в течение последних десятилетий, но вы по-прежнему сможете предсказать для каждого шара вероятность его положения на столе в любой момент времени. Статистика прошла долгий путь в исследовании вопросов неупорядоченной сложности.

Теперь разместите шары так, чтобы каждый из них оставался на одной линии и заставьте их двигаться так, чтобы каждый шар катился вдоль стенки по кругу, не касаясь другого шара, и математика окажется бессильной предсказать что-либо (рисунок 1). Для каждого отдельного шара можно рассчитать его путь, но описать систему в целом невозможно. Это – пример упорядоченной сложности. 

Можно с легкостью распространить этот пример до упорядоченных взаимодействий, отлично спланированная система может заставить шары взаимодействовать таким образом, что наблюдатель всегда будет знать, где находится каждый отдельный шар и каким будет характер взаимодействия в неопределенном будущем. Но и в этом случае, наблюдатель не сможет определить каким образом система пришла в такое состояние, но только предскажет, какими будут взаимодействия между разными шарами. 

Невозможно также будет описать систему как таковую, но описание будет ограничено только отдельными элементами. В то время, как неупорядоченная система может быть описана одной формулой или набором, упорядоченная система потребует набора формул.

Вивер придал большой вес науке организованной сложности: от ценообразования пшеницы до стабилизации курса валют. Подобно Виверу, инженер в современном обществе придает большое значение организованной сложности. Специалисты по статистике, биологи и те, кто старается построить совершенное общество, знают что без разрешения загадок организованной сложности им не обойтись.

Возможные решения задач организованной сложности

Итак, где мы находимся сейчас? Какой прогресс был достигнут в понимании организованной сложности? В последнее время были предприняты, по крайней мере, две серьезные попытки объяснения упорядоченной сложности в окружающем нас мире.³

Теория реляционного порядка — это современное направление в изучении сложности. В теории реляционного порядка положение и характеристики любого конкретного объекта имеют смысл только при их рассмотрении относительно других объектов. Например, существование атома имеет смысл только в связи с другими атомами, а пространство не существует, если оно не рассматривается по отношению к объектам внутри пространства. Процессы, в каком-то смысле, встроены в физический мир.⁴

Но все это требует ответа на один фундаментальный вопрос: откуда организованная сложность взялась?

Сказать, что она является частью природы, это все равно, что не сказать ничего. Предположение, что порядок — это неотъемлемая часть физического мира, и что этот врожденный порядок каким-то образом «возникает» внутри физического мира сам по себе, не отвечает на вопрос «Каким образом порядок стал частью физического мира?». Принятие подобных допущений не способствует объяснению упорядоченной сложности системы, а просто постулирует существование источника (альтернативный творец).

Еще одна попытка разрешить проблему, о которой можно упомянуть, это аналитика больших массивов данных. Предложенная компанией Google модель распределенных вычислений (the Map Reduced Paradigm) приведена на рис. 2. Она используется для поиска закономерностей внутри очень больших массивов данных. Большие массивы данных иногда рекламируются как ключ к пониманию и даже управлению общественным поведением. Как сказал Алекс Пентланд (Alex Pentland), однин из основоположников подхода больших массивов данных:

«Понимание систем «человек-машина» приведет к тому, что наши будущие социальные системы станут стабильными и безопасными. Мы выходим за рамки науки о сложности, науке о данных и науке о сети потому, что делаем людей составной частью этих систем. Большие объемы данных обещают обеспечить настоящее понимание систем, которые лежат в основе нашего технологического общества. Коль скоро мы начинаем понимать их, мы приобретаем способность построения систем более высокого качества. В результате можно будет создавать финансовые системы, которые не обрушатся, правительства, которые не погрязнут в бездействии, системы здравоохранения, которые будут эффективными и т.д. и т.п.»⁵

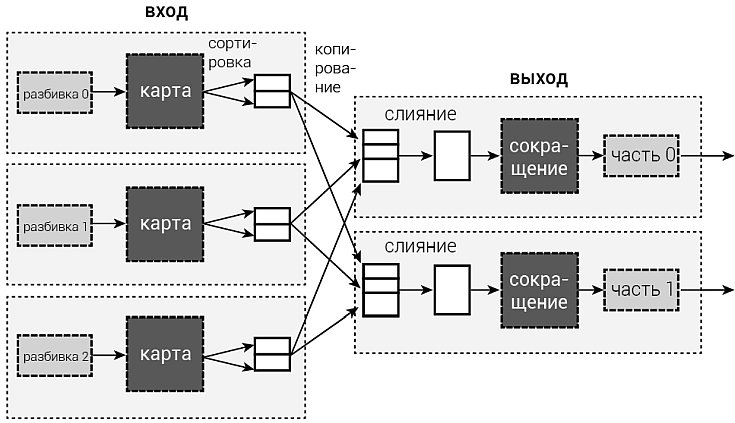Рисунок 2. Пример метода распределенных вычислений (the Map Reduced Paradigm).

Однако идею больших массивов данных ожидает серьезная проблема: этот подход работает не всегда. Внимательное рассмотрение слабых мест подхода и его допущений обнаруживает две причины возникновения такого препятствия. Во-первых, анализ больших объемов данных принимает допущение, что были собраны все правильные переменные и был запущен правильный алгоритм, который позволит обнаружить правильную тенденцию в правильное время. В итоге получается нагромождение слишком многих «правильностей». 

Во-вторых, подход больших данных принимает допущение о существовании эмерджентного порядка и направлен на его обнаружение путем массированных компьютерных вычислений. Сам подход не ставит целью объяснение упорядоченной сложности. Он попросту принимает допущение о том, что упорядоченная сложность является естественным свойством всех сложных систем, и потому используется для попыток обнаружить этот порядок.

Но что, если порядок не обладает эмерджентным свойством, как того требует большие объемы данных? В этом случае, поначалу нас может ожидать успех, за которым последует длительная раскрутка или затишье, означающее что тенденция уже достигла своей вершины. Как указывалось в одной статье в газете Financial Times, посвященной анализу большого количества данных, мы не должны (и не можем) принимать допущение, что всегда имеем в распоряжении все необходимые данные.⁶ 

Программа, предсказывающая локализацию и распространения гриппа в 2014 году (программа Flu), созданная компанией Google, потерпела провал и приводится в статье в качестве примера. Отдельные сообщения о ложных положительных тестах наводняют реальный мир, но, похоже, почти всегда игнорируются в «литературе». Газета The New York Times приводит девять проблем подхода больших объемов данных, включая тот факт, что «большие данные никогда не говорят нам какие из корреляций имеют смысл», указывая на риск обнаружить видимые ложные корреляции, которых на самом деле нет, и эффект эхо-камеры.⁷ 

Большие объемы данных исходят из предположения, что всякая сложность является упорядоченной, хотя такое допущение приведет к обнаружению ложного порядка даже в неупорядоченных массивах данных, что повлечет за собой ложные предсказания и неправильное управление миром. Подобная ошибка должна служить предупреждением при изучении упорядоченной сложности.

Увы, мы до сих пор не понимаем упорядоченную сложность. Круговая аргументация и предположение эмерджентных свойств также не могут помочь. Тогда в чем же суть проблемы?

В основе лежит материалистическое допущение, что все что есть, это только вещество. Если порядок есть, то так или иначе он проистекает из материи. В концепции больших данных эта идея далее развивается так: если вещество самоорганизуется, тогда таким же образом самоорганизуются и люди. 

Фактически, существование упорядоченной сложности становится доказательством реальности эмерджентности, а самоорганизация каким-то образом «встроена в ДНК» Вселенной (хотя Вселенная не имеет ДНК). Как постулировал один атеист по имени Краусс (Krauss):

«Каждый день внезапно появляются прекрасные и чудесные предметы, будь-то снежинки холодным, зимним утром или яркие радуги после предвечернего дождя. Но никто кроме самых ревностных фундаменталистов не станет предполагать, что каждый из этих предметов тщательно и с любовью, и что особенно важно, с целью, был сотворен божественным разумом. На самом деле, многие простые люди, да и ученые радуются, упиваясь нашей способностью объяснять, как снежинки и радуги спонтанно появляются, подчиняясь простым и элегантным законами физики».⁸

Многие математики и ученые, прокладывая путь через теории сложности, пытаются опровергнуть сотворение просто потому, что они не могут принять существование Творца. Наверное, как и Краусс, они считают, что ответ кроется в простом постулировании того, что каждая мыслимая вселенная, которая могла существовать, действительно существовала. 

Но с другой стороны, теория, которая объясняет каждый мыслимый исход, в конечном счете, не обладает способностью объяснять.

Заключение

Мы не можем решить проблемы упорядоченной сложности используя методы изучения беспорядка, мы не можем также объяснить порядок, наблюдаемый в природе, запихивая его под «ковер эмерджентности». Чтобы достичь прогресса в области упорядоченной сложности, необходимо идти прямиком к идее спланированного сотворения. 

Атеизм слеп к телеологии, материалистическое видение мира вынуждено отвергать любое понятие цели боясь «впустить Бога в дом». Но упорядоченная сложность на системном уровне, так или иначе, будет иметь смысл только в контексте телеологии, т.е. конечной цели.

Игнорируя сотворение путем допущения эмерджентности, атеистическая наука не видит плана творения, а потому не может даже начать приближаться к проблеме упорядоченной сложности. Это по настоящему вредит прогрессу науки из-за пустой траты исследовательского времени и денег, используемых на скитания по «темным переулкам», не давая науке задать главный вопрос: почему?